Business Value of Agile Manufacturing *

A factory produces finished products by performing a sequence of manufacturing steps (tasks) on supplied materials (inputs). In an automotive assembly plant, for example, numerous assembly tasks done in proper sequence convert a powertrain, electric components, body panels, instrument panel, paint and many other inputs into a finished vehicle. In modern plants, if the manufacturing tasks and machines are designed and controlled properly and the workers have suitable training, the plant can adjust rapidly to manufacture different products from the appropriate inputs.

Agile manufacturing refers to the ability of a factory to switch quickly from producing one product to producing another. Such flexibility can be beneficial and profitable, because a suitably flexible plant can respond quickly to changes in demand for its various products.

The analysis of agile manufacturing is of general industrial interest and offers many opportunities for industrial mathematics research. This project requires modeling and analyzing stochastic systems and optimization of such systems in a practical context that has immediate industrial value. These issues are very common in business decisions.

Automotive assembly plants are always flexible facilities that can at least manufacture the two-door, four-door and station wagon versions of a vehicle, install customer-selected options, etc. However, a higher level of flexibility, where an assembly plant produces different vehicle products (for example, two different models or sizes of an SUV), is the focus of this project.

Ford researchers have put significant effort into estimating variability in customer demand for our vehicles. We have developed demand distributions that predict (with stated probability) vehicle demand under various market conditions. From this stochastic demand data and other parameters, we want to configure our factories to meet the varying demands flexibly. We currently determine the degree of flexibility appropriate in designing a plant by using a simulation model to evaluate various product volume demand and flexibility scenarios. (The actual detailed design of flexible plants and their supply and delivery systems involves an enormous number of inter-related constraints and a great deal of data and is outside the scope of this project.)

The goal of this project is to estimate in advance, under simplifying assumptions, the value that flexible plants have for Ford. The desired analysis employs likely vehicle demand distributions, plant capacities and limitations, part commonality among vehicle products and, perhaps, other factors. Given this basic data, how should Ford run its product design and assembly business? What are the benefits if some parameters are changed - for example, increasing part commonality between vehicles?

Manufacturing flexibility is represented as a weighted ?production graph? where products (shown as nodes) are edge-connected to the plants (also nodes) that can assemble those products. A product node includes as data the demand for that vehicle. A plant node has as data the plant capacity (maximum total production of all vehicles). Each edge (connecting a product node to a plant node) carries as data the maximum amount of the product that can be built at the plant.

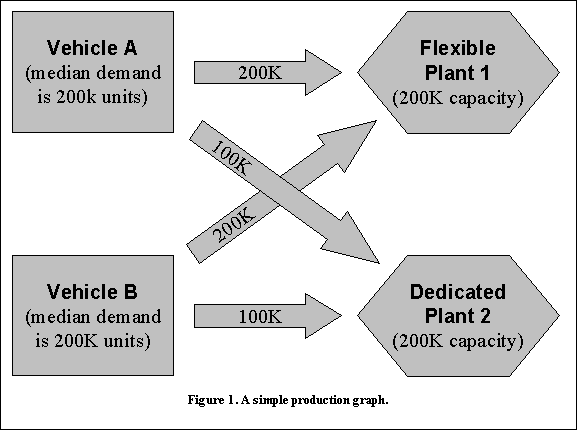
Example: Figure 1 shows a simple production graph: Plants 1 & 2 have assembly capacities of 200,000 vehicles (200k) each. Two products A & B, each with a median demand of 200k units, are to be assembled in these plants. Plant 1 can flex to produce any mix of products A and B up to its capacity of 200k units; this follows because the 200k edge weights indicate Plant 1 can build up to its full capacity of either vehicle. Plant 2 is more limited: it can produce at most half its full capacity of either vehicle. The two-plant system can produce up to 300k units of a "hot" vehicle, either A or B, if demand is that large (200k from plant 1 and 100k from plant 2).

Note that vehicle demand is given as the median of a distribution of demand data that Ford can furnish. Production graphs of business interest will include about 10-20 products and about 10 plants.

The project team would start with a production graph and other parameters that include at least:

• the expected distributions of demand for each vehicle product,
• values and correlations between product demand and expected profit per vehicle sold,
• total supply base (supplier) capacity for parts unique to each vehicle, and
• supply base capacity for common parts shared by specified vehicles.

We anticipate that the project team will apply these inputs to carry out some intermediate modeling of the agile manufacturing value-added to Ford Motor Company that is implicit in the inputs. We are open to discussion about other data that the project team feels would be relevant or valuable.

In addition to a research report, we seek, as a deliverable, an interactive Excel application (possibly including Visual Basic macro code) that combines the available models to automate the evaluation of a production graph. This application should also find optimal values for some of the relevant parameters, such as supply base capacity to produce given vehicles.

The Excel application should accept as inputs a production graph and the other parameters listed above that define the production system and consumer demand fluctuations to which the production system must respond. It should calculate the business value associated to the flexible system as a distribution of profit results over time. For example, the tool might simulate the operation of the given production system (cast in terms of net present value and other financial metrics) over a period of approximately five years, gauging the system's capability to respond to changing demand levels. During each year of the five-year period, an algorithm could attempt to optimize short-term profits by assignment of vehicle production within the constraints imposed by the system. The overall business value would be based on the profit distribution results from the full five-year period. Statistically relevant results could be produced either through Monte Carlo simulation of a large number of five-year periods, or possibly by analytic methods.

The Excel tool would be of greater value if it could find optimal or near-optimal values for a variety of components of the system. For example, given costs per level of supplier capacity, what is the optimal level of supply-base capacity to support each vehicle product? Another example: given effective costs of different amounts of component commonality between vehicles, what is the optimal level of commonality within a given portfolio of vehicles?

An even more advanced optimization capability would determine the best production graph given a variety of constraints. However, this latter capability could be very difficult to implement, and only indicates how advanced the tool could grow to be.

We hope that the project team will discover in the course of its work, rules of thumb revealing successful strategies for various flexibility conditions. These insights into the characteristics of higher-value flex-production systems might be properties of the associated production graphs, vehicle commonality levels, supply base characteristics, etc. and would be especially welcome. An example of such an insight is the conclusion of Jordan and Graves**, for a 10-product 10-plant system, that a production graph such that each product was produced by two plants, and each plant had two products, was almost as effective in producing a responsive production system as a fully flexible system in which any plant can build any product.

Researchers at Ford are already working in a number of the areas outlined above, and would be able to provide some guidance on practical approaches toward creating the Excel tool, and on insights already achieved in production systems aspects that are attractive.

* This summary prepared by R. E. Svetic, MSU; and M. Everson and P. M. Tuchinsky, Ford Research Laboratory, Ford Motor Company. The project team will be managed by Michigan State University Mathematics Professor Bruce Sagan.

** "Principles on the benefits of manufacturing process flexibility," William C. Jordan and Steven C. Graves, Management Science, 41 (4) April 1995, 577.

Back To the Top