-
Let
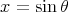 with
with 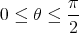 . Which of the following is
equivalent to the expression
. Which of the following is
equivalent to the expression 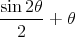 ?
?
a) arcsin x + x b) arcsin x + x 
c) 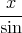 + x
+ x d) 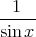 + x
+ x e) 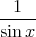 + x
+ x
|
Notice that ![]() and
and ![]() so that
so that
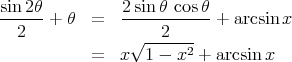
If you miss this question please review inverse trigonometric functions and double angle formulas. Also, see 6.4: Trigonometric Identities . |