-
Start at the origin in the plane. Move one-third of the way toward
the point (9, 12) and then turn
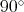 to the left and move 10 units.
What are the coordinates of your final position?
to the left and move 10 units.
What are the coordinates of your final position?
a) 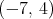
b) 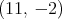
c) 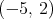
d) 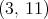
e) 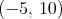
|
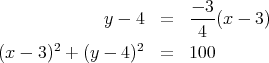
It follows that

It follows that the coordinates of the final position are ![]() .
.
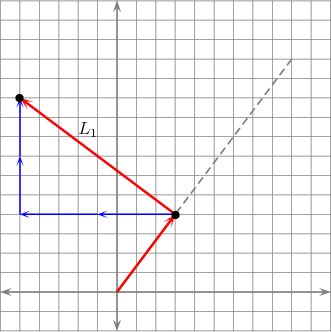
Perhaps is might be easier if we notice that the slope of ![]() is -3∕4 and that a triangle with base equal to 8 and
height equal to 6 has a hypotenuse of length 10. So from
is -3∕4 and that a triangle with base equal to 8 and
height equal to 6 has a hypotenuse of length 10. So from ![]() we move 8 units left and 6 units up (the blue
path).
we move 8 units left and 6 units up (the blue
path).
If you miss this question please review the Pythagorean Theorem. |